| Definitions | s = t, t  T, Type, T, Type,  , left + right, x:A , left + right, x:A  B(x), B(x),  b, {x:A| B(x)} , case b of inl(x) => s(x) | inr(y) => t(y), if b then t else f fi , Top, f^n, can-apply(f;x), b, {x:A| B(x)} , case b of inl(x) => s(x) | inr(y) => t(y), if b then t else f fi , Top, f^n, can-apply(f;x),  , A c , A c B, P & Q, x:A B, P & Q, x:A  B(x), P B(x), P   Q, P Q, P   Q, A Q, A  B, False, B, False,  A, A,  , n+m, a < b, Void, , n+m, a < b, Void,  x:A. B(x), S x:A. B(x), S  T, suptype(S; T), P T, suptype(S; T), P    Q, do-apply(f;x), {T}, f o g , True, Q, do-apply(f;x), {T}, f o g , True, 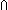 x:A.B(x), x:A.B(x),  T, T,  , ff, , ff,   b, p =b q, i <z j, i b, p =b q, i <z j, i  z j, (i = z j, (i =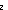 j), x =a y, null(as), a < j), x =a y, null(as), a < b, f(a), x f y, a < b, f(a), x f y, a < b, [d] b, [d] , p , p    q, p q, p   q, p q, p   q, tt, Unit q, tt, Unit |